Tim McGraw - Not a Moment Too Soon
Not a Moment Too Soon by Tim McGraw is the #3 album this week. I am not a big fan of modern country music. I like older country music: Johnny Cash, Dolly Parton, Willie Nelson are all great. Their songs are original and compelling. I find modern country a bit too trite and repetitive. The songs are so formulaic that someone put together a mix of songs all about the same things:
Not all modern country music is this bad. The worst country music is confined to the Bro-Country sub-genre. To an extent, the purveyors of this music are self-aware about this. For example, Beer Beer, Truck Truck (video) is a direct response to this criticism.
Not a Moment Too Soon is a bit too old to be Bro-Country and commit all the sins highlighted in the video above. Instead, it commits other sins including tackiness and racism!
- In It Doesn't Get Any Countrier Than This McGraw sings to his mother about his girlfriend and all the sex they've been having.
- In Indian Outlaw, McGraw (who is white) sings as if he was a Native American about his wigwam, paw-paw, and maw-maw. During one bridge there's a refrain that sounds like the Atlanta Braves theme.
- Refried Dreams is about being stuck in Mexico, destitute and missing a lost love. I'm not exactly sure what is refried about his dreams. Perhaps they're broken dreams, or unfulfilled, but what's refried about all that? Are they only refried because it sounds like refried beans? If so, is it basically only a slightly-racist pun? Hrm.
- Don't Take the Girl gives me painful whiplash. The first stanza is about a boy who wants to go fishing with his father, but doesn't want a girl to come along. No problem, that's cute enough. The next stanza the same boy is a teenager taking the same girl to the movies, when they are accosted by a stranger with a gun who wants to harm the girl. Wow, that's quite the turn. In the final stanza, the girl is dying during childbirth. Um, okay, that's, a way to end this song. I guess it tells a story but it's not a great one and it's not done in a way I find very artistic.
If you're wondering, in my opinion Americana is the inheritor to classic Country music.
Finally, I will not be listening to this album again.
more ...Above The Rim Soundtrack
This week I need to drop down to #3 to pick a new album. This is the soundtrack for the film Above the Rim, a movie I have not viewed. It has a middling rating on Rotten Tomatoes so I probably won't seek it out. It also doesn't seem to be on any streaming service I subscribe to, which makes the effort too much, anyway.
Listening to the album I think there are only a couple reasons why anyone would have bought the album:
- Tupac Shakur starred in the movie and there are three songs on the soundtrack that he presumably made for the film that were not available on any of his albums.
- The only genuine hit off the album is "Regulate" by Warren G. and Nate Dogg. The stand-alone album by Warren G., Regulate... G Funk Era, with the song didn't come out until June 1994, so the only way to buy the song at the time was to buy this album. My memory is a bit fuzzy, but I think I actually purchased a copy of the Warren G. album largely for this song.
All the other songs on this album are forgettable. There's a fairly pointless cover of the Al Green song "I'm Still in Love with You." When I write "pointless," I don't mean it didn't fit into the movie (it may have and I'll never know), I mean that the cover doesn't do anything the original doesn't already do. I'll bet the cover was cheaper to license. All the rest is pretty standard mid-90s hip-hop – songs where the artist states their name and the label they're signed to, etc. Granted, for a movie soundtrack, it's probably okay having some more generic music so it doesn't distract from what's happening on screen or with any dialog.
My final words are that this album can be left to the dusty piles of history. If you want to listen to "Regulate," listen to Warren G.'s album. If you want to listen to Tupac, listen to his multiple acclaimed albums which have better songs than what he made for the film.
more ...Pink Floyd - The Division Bell
Finding this album at #1 is both suprising and unsurprising. Pink Floyd was (is?) the greatest Prog Rock band of all time. Prog Rock reached peak popularity in the 70s, but by 1994 it was being supplanted by newer forms of Rock like Metal (Pantera) or Grunge (Soundgarden). The fact that The Division Bell was able to reach #1 is a testament to the greatness and popularity of Pink Floyd.
Among the Pink Floyd albums, this one definitely ranks behind their best, like Dark Side of the Moon, Wish You Were Here, and their double album The Wall. The track Comfortably Numb off of The Wall has two of the greatest guitar solos of all time in the same song. I've listened to this album two or three times and I can't think of any guitar solo that caught my attention. There are guitar solos, yes, but they don't have the same emotion.
I think that's the main problem with this album, it feels a bit too procedural. Pink Floyd had been popular for a couple decades by the mid-90s, and frankly, they were no longer starving musicians. Being a bit desperate and unloved can help a musician make great music. It is not bad music. Pink Floyd didn't suddenly forget how to make music, but there's nothing in this album that sparks emotion.
Not all albums an artist or group makes are going to be great. I'll still listen to Pink Floyd's great albums, but this one will probably get very few spins from me going forward.
more ...Bonnie Raitt - Longing in Their Hearts
One nice aspect of my 30 Years On project restart has been the balance of gender of musicians on the #1 list. It's been pretty well even between men and women, which is a good thing. This week Bonnie Raitt claims #1 outright with Longing in Their Hearts. According to the Wikipedia page, this album was released during the height of Bonnie Raitt's commercial popularity. Bonnie Raitt is most purely a Blues artist, and this album is definitely Pop-facing Blues.
None of the songs really challenge the listener, which is one of the definitions of Pop music. This is the kind of music that can be played to any audience and that's fine. Bonnie Raitt is a very good musician and this is a well made album. Indeed, in 1995 this album was nominated for the Album of the Year (which it didn't win against fairly weak competition) but it did win the award for "Best Pop Vocal Album."
My feelings towards this album are "meh." I'm fine with it exsiting, it doesn't offend me, nor does it excite me. It's nice. Nice is good. I'll probably never listen to this album again, not because it's bad, it most definitely is not, but because it does nothing for me, really.
more ...Pantera - Far Beyond Driven
Far Beyond Driven by Pantera is a kind of surprising album to reach #1. Pantera was a Groove Metal band, which despite the name, isn't very groovy in any way you might imagine. As per the Wikipedia, Groove Metal has a slower beat than Speed or Thrash Metal, which makes it groovy. It still features heavy guitar, raspy or screaming singing, and dark themes.
I find it surprising that the album made #1 because this isn't exactly mainstream music, now or 30 years ago. For better or worse I understand Mariah Carey being #1, but Pantera? Perhaps it was just luck and no big albums were released at the same time because next week this album dropped to #9, and then #19, #22, #25, etc. The #1 ranking was just a blip.
I could only take one listen to this album. I didn't like it at all. I like various kinds of metal, but not this kind.
more ...Counting Crows - August and Everything After
Ace of Base is back at #1 so I need to go down the list to find something to review. The first album I haven't already reviewed (I won't do R. Kelly) is at #4 with August and Everything After by Counting Crows. This is the second week in a row where I review an album I genuinely like. I won't ruin things, but I've gone through the albums I'll be listening to in the near future and some weeks are going to get rough.
This album has the song "Perfect Blue Buildings" with the lyrics:
Down on Virginia and La Loma
Where I've got friends who'll care for me
Counting Crows is from Berkeley, and this refers to the intersection of Virginia Street and La Loma Avenue in Berkeley. I've spent quite a bit of time near that intersection. When I was in middle or high school (can't remember precisely when; his family moved later due to divorce) I had a good friend who lived at 2708 Virginia St and in college I had some (other) friends who lived just next door at 2704 Virginia St, both of which are at that intersection. One of those college friends tells the story of walking home one day and encountering some lost-looking young women. He asked them "perfect blue buildings?" and they said "yeah." There were no blue houses at that intersection at that time (ca. 2000), so he replied "I think it's that one over there, it's got a newer paint job."
Through all of my undergraduate years at UC Berkeley (1998-2002) I bought student tickets to the home Men's basketball games. During this time team was fairly decent. They would win at home more often than not and only reliably lost to much better teams (UCLA, Stanfurd, and Arizona were the tough opponents). The games were fun to attend. Adam Durtiz, the lead singer of Counting Crows, was a regular at the games and I often saw him in the stands and hallways. I never asked for an autograph (selfies weren't a thing yet!). The main thing I took away from seeing him is that he's a pretty big guy, taller than me and husky.
I don't think I listened to Counting Crows all that much when the album came out. I think I was into more grunge rock than alternative rock (it's a small but important distinction!). Listening to this album doesn't conjure the same memories that other albums from this time might do. I'm certain I heard "Mr. Jones" on the radio when it was popular, and probably the other singles that came off the album. However my tastes in music have broadened since I was a teenager and according to Last.fm I've listened songs on this album almost 300 times. Like any kind of music I'm not always in the mood for this album, but sometimes I am and I continue to return to it.
more ...The European Decimal Comma is Wrong
There are many things we Americans do badly. We won't give ourselves a health care system that makes sense. We die on our roads more than other advanced countries. We kill ourselves and others with guns way more than any other country. We stubbornly stick to Imperial units when Metric units and its powers of ten make much more sense.
There are a few things we do better, however. American National Parks are far beyond anything any other country has. The Americans with Disabilities Act is superlative when compared to the feeble efforts of even the most advanced European countries. Our popular culture, for better or worse, is able to make it to even the most remote corners of the world.
I want to highlight one thing that many Europeans do that is
absolutely, 100% wrong, that Americans do right (or at least not incorrectly,
as I'll explain below).
In Europe, the number 12345/10 is written
1.234,5
while here in the land of freedom, we write it
1,234.5
Europeans are wrong because they are inconsistent. Like most of the world, they use a period "." to indicate the end of a sentence and a comma "," mid-sentence for phrasing. Periods are used between sentences to separate ideas, concepts, and thoughts. If we compare this to numbers, there's a big jump in concept from whole, countable integers, to less-than-one decimal numbers. Children learn whole numbers many years before learning decimals, and the whole time they're also learning to read. Learning that periods between sentences indicate a jump to a new thought or concept. Like sentences, Americans use periods to separate big ideas in numbers, specifically between integers and decimals. And this is why the European comma is wrong, and Americans are not wrong. Americans use a comma in a number to indicate groups of thousands (phrasing) and periods to indicate decimal numbers (new concept), which is consistent with how sentences are written.
There's really no defense to the European decimal comma, and frankly their refusal to fix it is just as bad as the many (many!) things Americans do wrongly.
more ...Soundgarden - Superunknown
For the first time since I restarted 30 Years On there is a #1 (*) album I have actually listened to multiple times, willingly. Superunknown by Soundgarden is one of the smash hit albums that makes up the Grunge wave that came out of Seattle in the early to mid-1990s. Since I started tracking my music plays, I have listened to some Soundgarden every year for the last 17 years (although 2015 was thin for some reason). As of this writing I have over 500 plays of Soundgarden.
I like to discover new music, and I'm still finding new artists to listen to. Last week a new album by Waxahatchee called Tigers Blood was released and it's great. But there's always going to be a place for the music I listened to as a teenager. A fair number of songs from this album still get steady radio airplay: Black Hole Sun, Fell on Black Days, and Spoonman. The whole album remains worth listening to by me, and by you, forever.
If you go to the Grunge link at Wikipedia, the second paragraph mentions a list of popular Grunge bands and their breakout hit albums: Nevermind by Nirvana, Ten by Pearl Jam, Dirt by Alice in Chains, Core by Stone Temple Pilots, and Superunknown. The (original) lead singers of these bands, except for Pearl Jam, all died untimely early deaths due to drugs or suicide. I guess that says something about Grunge musicians. Oh well, I can enjoy the music without succumbing to the same fate.
(*) The #2 album this week is The Downward Spiral. This was a good week for music 30 years ago!
more ...Toni Braxton - Toni Braxton
A different #1 album has topped the charts: Toni Braxton by (betcha can't guess) Toni Braxton. Interestingly, it was released 8 months "ago" on July 13, 1993; apparently it experienced a bounce in sales to bring it back to the top "now."
This album is very 90s R&B. It is very tightly produced by Babyface and Toni Braxton is an excellent singer. The songs are all as you would expect, about love and relationships.
Listening through the album I don't feel like any particular song stands out, which is both a good and bad thing. If you're in the mood for some 90s R&B, this delivers. It's 53 minutes and 29 seconds of smooth beats and harmonies which sometimes is exactly what is wanted. Let's just say it's not the kind of music that puts you in the mood to do a workout or spring clean the house.
I must have heard some of these songs on the radio 30 years ago because this album did very well, but honestly I can't remember. None of them seem familiar, in particular, but they all seem familiar. I'm more confident that I've not heard them at all within the last decade or more.
I am not often in the mood for 90s R&B and, while this album is not bad, per se, it's not really something I reach for often, or, ever. Ok, sometimes I need a dose of End of the Road, but only sometimes.
more ...Kid Arts
Here's a bunch of various kid art for March 2024. I have no idea how old some of it is. Enjoy!


















 more ...
more ...
Ace of Base - The Sign
Music Box is still the #1 album, but the #2 album is by R. Kelly, someone I'm going to stay away from, so we'll slide down to the #3 album, The Sign by the Swedish band Ace of Base. According to my last.fm scrobbling history, before today I had listened to Ace of Base exactly two times, probably as part of an algorithmic mix on a streaming service. I definitely remember hearing a few of these songs on the radio when this album came out and was popular, but I can't say I could remember the last time I heard it on the radio. Clearly, they're not my favorite band.
But luckily for them, my tastes, and perhaps American radio, the world has different tastes and they are the third most popular Swedish band in history, and have sold many millions of records. Don't worry about them.
Ace of Base is basically pure pop music, which isn't a bad thing. Their music is entertaining and enjoyable in the way pop music should be. It's obviously very synthesized, the horns in the beginning of "All That She Wants" are unambiguously fake. But that's the appeal of pop, right? Music that's tight, clean, and keeps the surprises to a minimum. Pop should be very danceable. The biggest hit off the record (in the United States), the eponymous "The Sign" fits this bill with a catchy driving beat. Many of the songs on this album were on their first album "Happy Nation" which did not make an impression in the US. This includes the title track of that album "Happy Nation" that didn't chart at all in the US. Curiously, "Happy Nation" appears to have a recent (relative) surge in plays according to last.fm, but the other songs off this album remain more popular overall.
My summary is that this music is not my favorite, but it's not bad. Now that I've been reminded of it, maybe when I'm in the mood for some pop, I'll think of them. We'll see!
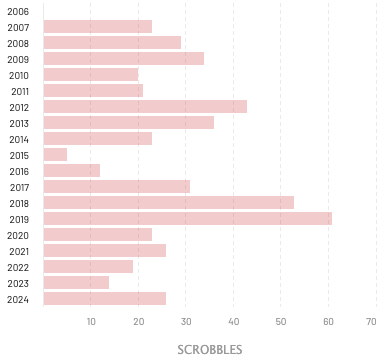
more ...Finale for last.fm
Since 2006 I've engaged in a bit of navel-gazing and tracked my music listening using last.fm. By running an application on your computer or phone, or linking a streaming service to last.fm (e.g. Tidal and Spotify support this), the service keeps track of what songs you listen to. The act of recording a song listen is called a "scrobble." However, it's always kind of bugged me that you can't scrobble in all situations, like when listening to an internet radio station or terrestrial radio.
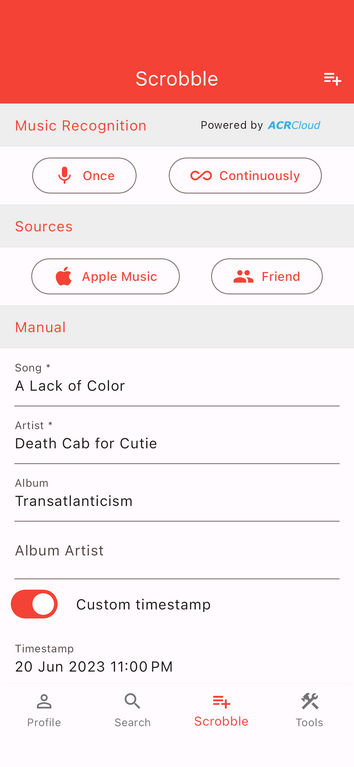
Recently I discovered the Finale app that does exactly this: it not only allows you to manually enter songs, it includes Shazam-like ability to listen to songs and identify them for you, and if you like, then scrobble the song. It has a "continuously listen" mode which despite the name means that once a minute it wakes up and listens for any new song you're listening to and scrobbles for you.
Somewhat related, I would like to recommend The Colorado Sound, a music radio station operated by a local NPR affiliate. It's as commercial-free as NPR is (limited to "supported by" messages) and has a very wide and eclectic selection of music. Using the Finale app while I listen to their internet stream allows me to keep track of what they're playing, and if I hear something I like, I can revisit that song/artist. You should check it out!
more ...