A couple days ago I was browsing the internet on astrophysical topics, when I came across Sir Arthur Stanley Eddington's wikipedia page. He's best known for the Eddington limit, which describes the luminosity limit of a star as a function of its mass. Near the bottom of his page linked above, there is a description of the "Eddington number," which for any person is the greatest number of bike rides they done which have been that at least that number in miles long. From the wikipedia page:
The Eddington Number in this context is defined as E, the number of days a cyclist has cycled more than E miles. For example an Eddington Number of 70 would imply that a cyclist has cycled more than 70 miles in a day on 70 occasions.
This is very similar to the Erdős number and the h-index, which measure a scientists publishing impact. I don't have an Erdős number, nor an h-index, but I do have an Eddington number. And since I have a nice GPS database of my rides, I figured I could easily calculate it.
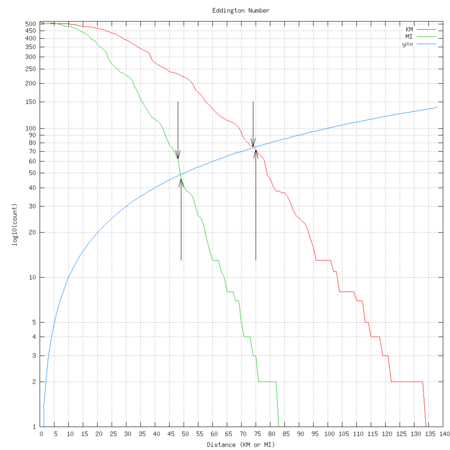
Above shows two Eddington calculations, in miles and in kilometers. The curved blue line is x=y, and it's curved because the y axis is using a logscale. Where the blue line intersects the Eddington lines is my Eddington number. The downward arrows show my actual integer Eddington numbers (48 for miles, 74 for kilometers), while the upward arrows show that 49 and 75 aren't above the blue line, and thus aren't my Eddington numbers. Since the definition is in miles, my true number is 48, but the kilometer calculation shows that the number is also a function of your unit.
Unfortunately, I don't have records before I got my GPS, so my true Eddington number is surely larger.